How Bloom Filters Work

In this tutorial, we are going to discuss about How Bloom Filters Work. Bloom filters are probabilistic data structures used for testing set membership, particularly in scenarios where memory or storage resources are limited. They provide a space-efficient way to represent a large set of items while allowing for false positives but not false negatives. Here’s a step-by-step explanation of how Bloom filters work:

1. Initialization

A Bloom filter is initialized with a bit array of size m, typically initialized to all zeros. The size of the bit array (m) determines the capacity of the Bloom filter and is chosen based on the expected number of elements in the set and the desired false positive rate.
Additionally, k hash functions are chosen. These hash functions are typically independent and uniformly distributed, and they generate k different hash values for each element added to the Bloom filter.

2. Components: Bit Array and Hash Functions

A Bloom filter consists of two primary components: a bit array and a collection of hash functions. The bit array is a fixed-size sequence of bits (0 or 1) initialized to all zeroes.
The number of hash functions, usually denoted as k, determines how many positions in the bit array an element maps to.
The hash functions should ideally be independent and uniformly distributed to minimize the probability of false positives.

3. Adding Elements to the Filter

To add an element to the Bloom filter, the element is passed through each of the k hash functions, generating k different hash values.
Each hash value corresponds to a position in the bit array. The bits at these positions are then set to 1.
This process is repeated for all elements that need to be added to the filter.
For example, following Bloom filter consists of 20 bits and uses three (k=3) hash functions H1, H2, and H3.

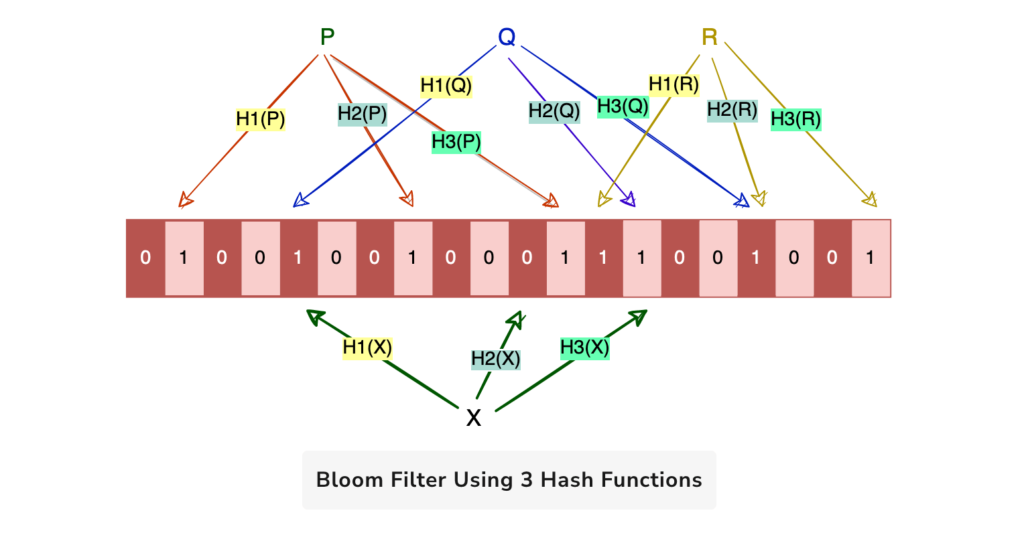
4. Testing Membership

To test whether an element is in the set, the element is passed through each of the k hash functions again, producing k hash values.
The Bloom filter checks whether the bits at all of the corresponding indices in the bit array are set to 1. If they are, the Bloom filter returns “possibly in set.”
If any of the bits at the corresponding indices are 0, the Bloom filter definitively concludes that the element is not in the set.

5. False Positives

Bloom filters can produce false positives, meaning they may incorrectly report that an element is in the set when it is not. False positives occur when multiple elements hash to the same set of bits in the bit array.
The probability of false positives depends on several factors, including the size of the bit array (m), the number of hash functions (k), and the number of elements added to the Bloom filter (n).
False positives can be controlled by adjusting these parameters based on the desired false positive rate and the expected number of elements in the set.

6. Optimizations

Bloom filters can be optimized by choosing appropriate values for m and k based on the expected number of elements in the set and the desired false positive rate.
Cryptographic hash functions or specialized hash functions may be used to improve the distribution of hash values and reduce the likelihood of collisions.
Bloom filters can also be combined with other techniques, such as counting Bloom filters or cuckoo filters, to further improve performance and reduce false positives.

In summary, Bloom filters provide a space-efficient and probabilistic method for testing set membership. While they can produce false positives, Bloom filters are useful in scenarios where memory or storage resources are limited and the trade-off between space and accuracy is acceptable.

That’s all about the How Bloom Filters Work. If you have any queries or feedback, please write us email at contact@waytoeasylearn.com. Enjoy learning, Enjoy system design..!!

How Bloom Filters Work