Introduction to Arrays
In this tutorial, we are going to discuss about the Introduction to Arrays. Array is one of the fundamental data structures and is used extensively in software development. Arrays provide a means of storing and organizing data in a systematic, computer-memory-efficient manner. Arrays provide a way to store and access multiple elements efficiently using indices.
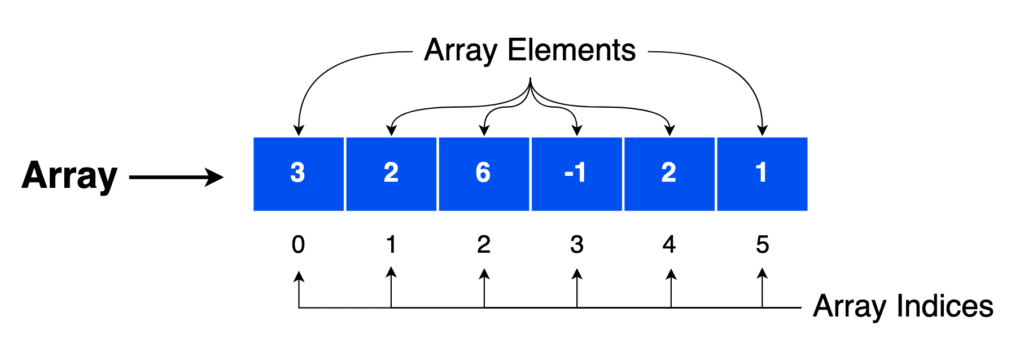
Essentially, an array is a collection of elements, each identified by an array index. The array elements are stored in contiguous memory locations, meaning they are stored in a sequence.
Static vs. Dynamic Sized Arrays
Arrays can be categorized into 2 types based on whether their size can change during runtime: static-sized arrays and dynamic-sized arrays.
Static-sized Arrays
Static-sized arrays have a fixed size, determined at compile time. Once declared, the size of a static array cannot be changed.
Characteristics
- Fixed Size: The number of elements the array can hold is defined when the array is created and cannot be altered.
- Memory Allocation: Memory for the array is allocated on the stack (in most programming environments), making allocation and deallocation fast.
- Performance: Accessing elements in a static array is fast because elements are stored contiguously in memory, enabling efficient indexing.
Example Use Case: Storing a predefined number of elements, such as the days of the week.
Here are how static arrays are declared in different languages:
Java
int[] staticArray = new int[5]; // Static array with a fixed size of 5
staticArray[0] = 1; // Assigning value to the first elementPython 3
from array import array
# Static Array (Using the array module for strictly typed arrays;
# however, lists are more commonly used and can be considered dynamic.)
staticArray = array('i', [0]*5) # Array of integers with a fixed size of 5
staticArray[0] = 1Golang
var staticArray [5]int // Static array with a fixed size of 5
staticArray[0] = 1 // Assigning value to the first elementC++
int staticArray[5]; // Static array with a fixed size of 5
staticArray[0] = 1; // Assigning value to the first elementDynamic-sized Arrays
Dynamic-sized arrays can change size during runtime. They can grow or shrink as needed, offering more flexibility.
Characteristics
- Resizable: The array can adjust its size at runtime to accommodate more (or fewer) elements than initially declared.
- Memory Allocation: Memory for dynamic arrays is typically allocated on the heap, which allows them to have a flexible size but also means that memory management (allocation and deallocation) is more complex and slightly slower.
- Efficiency Considerations: While dynamic arrays provide flexibility, resizing operations (like increasing the array’s size) may require allocating new memory and copying existing elements to the new location, which can be costly in terms of performance.
Example Use Case: Storing a list of user inputs where the number of inputs is not known in advance.
Here are how dynamic arrays are declared in different languages:
Java
ArrayList<Integer> dynamicArray = new ArrayList<>(); // Dynamic array
dynamicArray.add(1); // Adding an elementPython 3
dynamicArray = [] # Dynamic array (list in Python)
dynamicArray.append(1) # Adding an elementGolang
dynamicArray := make([]int, 0) // Dynamic array (slice in Go)
dynamicArray = append(dynamicArray, 1) // Adding an element#include <vector>
std::vector<int> dynamicArray; // Dynamic array
dynamicArray.push_back(1); // Adding an elementComparison
- Flexibility: Dynamic arrays offer more flexibility than static arrays because they can grow or shrink during runtime.
- Performance: Static arrays often provide better performance for fixed-size collections due to their contiguous memory allocation and absence of resizing overhead.
- Memory Management: Static arrays generally require less manual memory management than dynamic arrays, as the latter may involve explicit allocation and deallocation to manage memory on the heap.
- Usage: The choice between static and dynamic arrays depends on the specific requirements of the application, including whether the size of the data collection is known ahead of time and how much variability there is in the number of elements to be stored.
Basic Concepts and Operations
1. Accessing Elements
Each element within an array can be accessed using its index, which denotes the position of the element in the array. The indices typically commence from zero, meaning the first element is accessed using array[0], the second with array[1], and so forth. Accessing elements in an array is an O(1) time complexity operation, as it directs to the precise memory location without requiring iteration through other elements.
2. Inserting Elements
The insertion of elements can be executed in multiple ways, depending upon the requisite application:
- At the End: An element may be inserted at the end of an array, which is usually an
O(1)operation. - At a Specific Index: If insertion is desired at a particular index, subsequent elements must be shifted to make room, escalating the time complexity to
O(n)in the worst case.
3. Deleting Elements
Deleting elements also comes with its own set of considerations:
- From the End: Removing an element from the end is typically an
O(1)operation, as it doesn’t require repositioning of other elements. - From a Specific Index: Deletion from a particular index requires shifting the subsequent elements to fill the gap, making it an
O(n)time complexity operation.

4. Searching Elements
Searching involves identifying the index of a specified element. Without any additional information or constraints, a linear search is performed, scanning each element until the sought one is found, associating it with an O(n) complexity. However, if the array is sorted, binary search can be employed, reducing the complexity to O(logn).
5. Updating Elements
Updating an element at a specified index can be achieved directly and is generally an O(1) operation, since it entails altering the value at a specified memory location, which is obtained without scanning through additional elements.
Properties of Arrays
1. Memory Allocation
Arrays are defined by contiguous memory allocation, implying that each element is stored in adjacent memory locations. This allows arrays to provide constant-time access to any element using its index, as the memory address of any element can be calculated using the base address, the size of an element, and the index of the element.
Mathematically expressed, if B represents the base address, I denotes the index, and S signifies the size of each element, the address A of the element at index can be computed as:
A = B + (I * S)2. Indexing
Arrays utilize zero-based indexing, where the first element is accessed with the index 0, the second with index 1, and so on. Indexing enables direct access to any element within the array, thereby facilitating operations like search, update, and direct access with a consistent time complexity of (O(1)).
Being Mindful About Arrays in Coding Interviews
Arrays can be seemingly straightforward, but handling them proficiently during an interview involves keeping numerous nuances and potential pitfalls in mind. Here are some things that interviewees should be cautious about when dealing with arrays during coding interviews:
1. Validating Assumptions
- Duplicates: Always clarify if duplicate values are allowed. Understand and communicate how duplicates might affect your approach.
- Sorted/Unsorted: Check whether the array is sorted or not, as certain algorithms (like binary search) require sorted arrays.
2. Boundary Conditions
- Index Out of Bounds: Always ensure that your code never tries to access an index outside of the array’s bounds. Use condition checks to prevent this common error.
- Negative Indices: In certain languages like Python, negative indices access elements from the end of the array. Be cautious and deliberate in your use of them.
3. Efficiency Concerns
- Slicing and Concatenating: Remember slicing and concatenating can take
O(n)time. Be careful with these operations as they introduce significant time complexity into your solution. - In-place vs. Extra Space: Consider whether creating a new array is necessary or if you can manipulate the existing array in place to save space.
4. Variable Naming and Loop Indices
- Descriptive Variables: Use descriptive variable names to keep your code readable and your logic clear, even under interview pressure.
- Loop Indices: Be mindful of your use of loop indices, ensuring that loops end at the correct conditions to prevent off-by-one errors.
5. Algorithm Choice and Complexity
- Time and Space Complexity: Be conscious of the time and space complexity of the algorithms you choose and be prepared to discuss and justify them.
- Nested Loops: Be wary of introducing nested loops, which can rapidly escalate time complexity (e.g., to O(n^2)).
6. Testing
- Corner Cases: Test your solutions with edge cases (e.g., empty arrays, single-element arrays, arrays with all identical elements) to ensure robustness.
- Various Inputs: Test with both typical and edge cases to ensure your solution handles all possible scenarios adeptly.
7. Handling Zeros and Negatives
- Always check and clarify how to handle zeros and negative numbers in array problems. This is especially crucial in problems related to product or sum.
8. Modification During Iteration
- Be cautious when modifying an array as you iterate through it, as this can introduce bugs or unintended behaviors. Sometimes iterating backwards or using a separate array to store modifications can circumvent these issues.
9. Array Methods Familiarity
- Be familiar with the array methods provided by the language you’re using and understand their time and space complexities.
10. Partial Results
- Intermediate Variables: Consider whether storing intermediate results (e.g., prefix sums or suffix products) might optimize repeated calculations.
- Multiple Passes: Weigh the pros and cons of making multiple passes through the array if it simplifies and optimizes the overall algorithm.
11. Parallel and Reverse Iteration
- Remember that sometimes iterating through an array from the end or through two arrays in parallel can be the key to an optimal solution.
12. Understanding Problem Requirements
- Always make sure that you’ve understood the problem requirements and constraints correctly to avoid working toward an incorrect solution.
Approaching array problems with these considerations in mind will help you navigate through solutions more accurately and efficiently during interviews. Always communicate your thought process clearly and don’t hesitate to ask clarifying questions to ensure you’re on the right path. Practice, introspection, and iteration on various problems will deepen your understanding and enhance your problem-solving skills with arrays.
That’s all about the Introduction to Arrays. If you have any queries or feedback, please write us email at contact@waytoeasylearn.com. Enjoy learning, Enjoy Data Structures.!!