Algorithm Complexity
In this tutorial, we are going to discuss about the algorithm complexity. The complexity of an algorithm is a measure of the amount of time and/or space required by an algorithm for an input of a given size (n). Suppose X is an algorithm and n is the size of input data, the time and space used by the algorithm X are the two main factors, which decide the efficiency of X.
1. Time Complexity
Every algorithm requires some amount of computer time to execute its instruction to perform the task. The time complexity of an algorithm represents the amount of time required by the algorithm to run to completion. Time requirements can be defined as a numerical function T(n), where T(n) can be measured as the number of steps, provided each step consumes constant time.
For example, the addition of two n-bit integers takes n steps. Consequently, the total computational time is T(n) = c * n, where c is the time taken for the addition of two bits. Here, we observe that T(n) grows linearly as the input size increases.
Generally, the running time of an algorithm depends upon the following
- Whether it is running on a Single processor machine or a Multiprocessor machine.
- Whether it is a 32-bit machine or 64-bit machine
- Read and Write speed of the machine.
- The time it takes to perform Arithmetic operations, logical operations, return value and assignment operations, etc.,
- Input data
Note
When we calculate time complexity of an algorithm, we consider only input data and ignore the remaining things, as they are machine-dependent. We check only, how our program is behaving for the different input values to perform all the operations like Arithmetic, Logical, Return value and Assignment etc.
Calculating Time Complexity of an algorithm based on the system configuration is a very difficult task because, the configuration changes from one system to another system. To solve this problem, we must assume a model machine with specific configuration. So that, we can able to calculate generalized time complexity according to that model machine.
To calculate time complexity of an algorithm, we need to define a model machine. Let us assume a machine with following configuration.
- Single processor machine
- 32-bit Operating System machine
- It performs sequential execution
- It requires 1 unit of time for Arithmetic and Logical operations
- It requires 1 unit of time for Assignment and Return value
- It requires 1 unit of time for Read and Write operations
Now, we calculate the time complexity of following example code by using the above defined model machine. Consider the following piece of code.
int multiply (int a, int b){
return a*b;
}In the above sample code, it requires 1 unit of time to calculate a*b and 1 unit of time to return the value. That means, totally it takes 2 units of time to complete its execution. And it does not change based on the input values of a and b. That means for all input values, it requires the same amount of time i.e. 2 units.
Note
If any program requires a fixed amount of time for all input values then its time complexity is said to be Constant Time Complexity. Let us consider another example,
int sum(int A[], int n){
int sum = 0, i;
for(i = 0; i < n; i++ {
sum = sum + A[i];
}
return sum;
}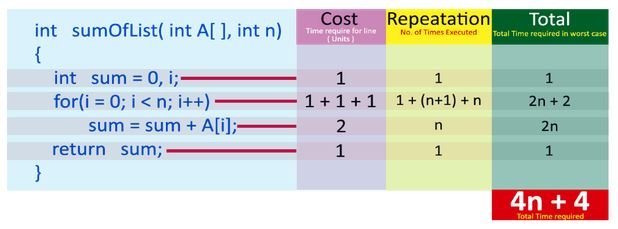
In above calculation
Cost is the amount of computer time required for a single operation in each line.
Reputation is the amount of computer time required by each operation for all its repetitions.
Total is the amount of computer time required by each operation to execute.
So above code requires ‘4n+4’ Units of computer time to complete the task. Here the exact time is not fixed. And it changes based on the n value. If we increase the n value then the time required also increases linearly. Totally it takes ‘4n+4’ units of time to complete its execution and it is Linear Time Complexity.
Note
If the amount of time required by an algorithm is increased with the increase of input value then that time complexity is said to be Linear Time Complexity.
2. Space Complexity
When we design an algorithm to solve a problem, it needs some computer memory to complete its execution. For any algorithm, memory is required for the following purposes.
- Memory required to store program instructions
- Memory required to store constant values
- Memory required to store variable values
- And for few other things
Space complexity of an algorithm can be defined as “Total amount of computer memory required by an algorithm to complete its execution is called as space complexity of that algorithm.” Generally, when a program is under execution it uses the computer memory for THREE reasons. They are as follows.
Instruction Space: It is the amount of memory used to store compiled version of instructions.
Environmental Stack: It is the amount of memory used to store information of partially executed functions at the time of function call.
Data Space: It is the amount of memory used to store all the variables and constants.
Note
When we want to perform analysis of an algorithm based on its Space complexity, we consider only Data Space and ignore Instruction Space as well as Environmental Stack. That means we calculate only the memory required to store Variables, Constants, Structures, etc.,
To calculate the space complexity, we must know the memory required to store different datatype values (according to the compiler). For example, the C Programming Language compiler requires the following.
- 2 bytes to store Integer value,
- 4 bytes to store Floating-Point value,
- 1 byte to store Character value,
- 8 bytes to store double value.
int square(int a){
return a*a;
}In the above piece of code, it requires 2 bytes of memory to store variable a, and another 2 bytes of memory is used for the return value. This means, totally it requires 4 bytes of memory to complete its execution. And this 4 bytes of memory are fixed for any input value of ‘a’. This space complexity is said to be Constant Space Complexity.
Note
If an algorithm requires a fixed amount of space for all input values then that space complexity is said to be Constant Space Complexity.
Let us consider the following piece of code.
int sum(int A[], int n){
int sum = 0, i;
for(i = 0; i < n; i++) {
sum = sum + A[i];
}
return sum;
}In the above piece of code, it requires
- ‘n*2’ bytes of memory to store array variable ‘a[]’
- 2 bytes of memory for integer parameter ‘n’
- 4 bytes of memory for local integer variables ‘sum’ and ‘i’ (2 bytes each)
- 2 bytes of memory for the return value.
That means, totally it requires ‘2n+8’ bytes of memory to complete its execution. Here, the amount of memory depends on the input value of ‘n’. This space complexity is said to be Linear Space Complexity.
Note
If the amount of space required by an algorithm is increased with the increase of input value, then that space complexity is said to be Linear Space Complexity.
That’s all about the Algorithm Complexity. If you have any queries or feedback, please write us email at contact@waytoeasylearn.com. Enjoy learning, Enjoy Data Structures.!!